基本介紹
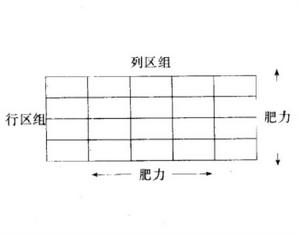
雙向區組,在—個方向上的區組作為一維區組稱做“ 行區組”,在另—方向上的區組作為一維區組,稱做“ 列區組”。如,農田試驗按肥力對田地在兩個方向上的區組,可以形象地表示為
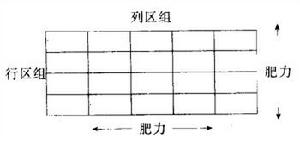 圖1
圖1其中每行和每列的幾個小區構成行區組和列區組。
同樣可以考慮多向區組。按一個標誌劃分的區組稱做“單向區組”。單向和多向區組的區別在於,前者各小區的條件相同,而後者則不然。隨機化區組和不完全區組都是單向區組。
實驗設計
農業試驗一般是田間試驗,受環境條件的影響較大,其中土壤差異是最重要的影響因素,故田間試驗設計將區組分為縱向區組和橫向區組,從而控制縱橫兩個方向的土壤差異,提高試驗的精確度。
雙向區組作因素的設計
1.設計方法
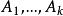 雙向區組
雙向區組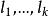 雙向區組
雙向區組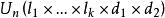 雙向區組
雙向區組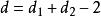 雙向區組
雙向區組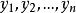 雙向區組
雙向區組設試驗中有k個因素 ,其對應水平數分別為 ;又有2個方向的隨機區組A、B,分別對應有d、d個狀態,為表達方便,不妨假設k個因素為定量變數,隨機區組A、B為定性變數。我們以混合型均勻設計表中選出帶有s=k+2列的 均勻表,可假設表中前k列對應k個連續變數;表中後2列可安排區組因素,並要求n>k+d+1,其中 。試驗設計如表1,為保證此兩因素為完全試驗的組合,可通過擬水平方法對區組水平作相應的處理,然後安排n個試驗,得到n個結果 。
| 1 | 2 | 3 |  雙向區組 雙向區組 | 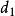 雙向區組 雙向區組 | |
| 1 | 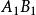 雙向區組 雙向區組 | 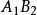 雙向區組 雙向區組 | 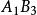 雙向區組 雙向區組 |  雙向區組 雙向區組 | 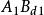 雙向區組 雙向區組 |
| 2 | 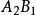 雙向區組 雙向區組 | 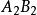 雙向區組 雙向區組 | 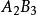 雙向區組 雙向區組 |  雙向區組 雙向區組 | 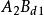 雙向區組 雙向區組 |
 雙向區組 雙向區組 |  雙向區組 雙向區組 |  雙向區組 雙向區組 |  雙向區組 雙向區組 |  雙向區組 雙向區組 |  雙向區組 雙向區組 |
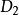 雙向區組 雙向區組 | 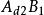 雙向區組 雙向區組 | 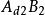 雙向區組 雙向區組 | 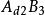 雙向區組 雙向區組 | 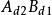 雙向區組 雙向區組 |
2.試驗數據的統計分析
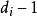 雙向區組
雙向區組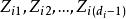 雙向區組
雙向區組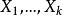 雙向區組
雙向區組與處理單區組因素的統計分析方法一樣,首先進行數量化處理,將2個區組因素之狀態,分別化成( )個相對獨立的偽變數 ,其中i=1,2.將這總共d=d+d-2個偽變數與相應的k個定量變數 ,一起建立多元回歸方程。為此,要注意對均勻設計表進行挑選,以保證各類效應不蛻化。根據實際需要可考慮建立以下模型:
1)一階線性模型,即考察如下的回歸方程:
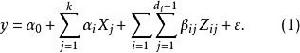 雙向區組
雙向區組解出回歸係數,找出最佳狀態組合,並算出最大估計值。
2)二次回響曲面模型(考慮一些互動效應,和一些連續變數的高次效應)。考察如下的回歸方程
通過數據分析,在試驗結果的變異中剖分出橫向區組、縱向區組、組合處理問的變異以及隨機誤差的變異,並找出最佳化的因素組合。
實例1 為了解2種肥料對某一新作物的影響,通過試驗找出它們適宜肥料拌種的方法與用量,摸索增產規律。種子拌肥量的水平如下:X磷肥(g/單位面積)分為12個水平:{200,220,240,260,280,300,320,340,360,380,400,420};X腐植酸銨(g/單位面積)分為6個水平:{200,240,280,320,360,400}。
考慮土地的差異設定橫向B(4塊)和縱向A(3塊),選用的均勻設計表如表2,根據表2均勻表前4列安排試驗,得到的試驗結果如表3。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| 1 | 1 | 1 | 1 | 2 | 3 | 1 | 2 |
| 2 | 2 | 2 | 2 | 3 | 2 | 2 | 1 |
| 3 | 3 | 3 | 3 | 2 | 1 | 1 | 2 |
| 4 | 4 | 4 | 4 | 3 | 1 | 2 | 1 |
| 5 | 5 | 5 | 1 | 1 | 2 | 2 | 2 |
| 6 | 6 | 6 | 2 | 3 | 2 | 1 | 1 |
| 7 | 7 | 1 | 3 | 1 | 1 | 1 | 1 |
| 8 | 8 | 2 | 4 | 3 | 3 | 2 | 1 |
| 9 | 9 | 3 | 1 | 1 | 3 | 2 | 2 |
| 10 | 10 | 4 | 2 | 2 | 2 | 1 | 2 |
| 11 | 11 | 5 | 3 | 1 | 1 | 1 | 1 |
| 12 | 12 | 6 | 4 | 2 | 3 | 2 | 2 |
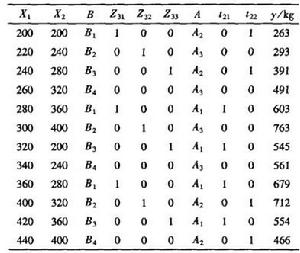 表2
表2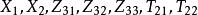 雙向區組
雙向區組考慮變數 ,用SAS軟體包求解建立回歸方程為:
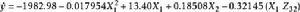 雙向區組
雙向區組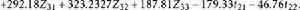 雙向區組
雙向區組F=2 021.757>F,差異極顯著。由上式可求得最佳狀態組合為X=371.4,X=400,B取1,A取3,此時可獲最大估計值。