遺傳[生物進化過程的計算模型]

遺傳算法（Genetic Algorithm）是模擬達爾文生物進化論的自然選擇和遺傳學機理的生物進化過程的計算模型，是一種通過模擬自然進化過程搜尋最優解的方法。遺傳算法是從代表問題可能潛在的解集的一個種群（population）開始的，而一個種群則由經過基因（gene）編碼的一定數目的個體(individual)組成。每個個體實際上是染色體(chromosome)帶有特徵的實體。染色體作為遺傳物質的主要載體，即多個基因的集合，其內部表現（即基因型）是某種基因組合，它決定了個體的形狀的外部表現，如黑頭髮的特徵是由染色體中控制這一特徵的某種基因組合決定的。因此，在一開始需要實現從表現型到基因型的映射即編碼工作。由於仿照基因編碼的工作很複雜，我們往往進行簡化，如二進制編碼，初代種群產生之後，按照適者生存和優勝劣汰的原理，逐代（generation）演化產生出越來越好的近似解，在每一代，根據問題域中個體的適應度（fitness）大小選擇（selection）個體，並藉助於自然遺傳學的遺傳運算元（genetic operators）進行組合交叉（crossover）和變異（mutation），產生出代表新的解集的種群。這個過程將導致種群像自然進化一樣的後生代種群比前代更加適應於環境，末代種群中的最優個體經過解碼（decoding），可以作為問題近似最優解。

運算過程

遺傳算法（Genetic Algorithm）是一類借鑑生物界的進化規律（適者生存，優勝劣汰遺傳機制）演化而來的隨機化搜尋方法。它是由美國的J.Holland教授1975年首先提出，其主要特點是直接對結構對象進行操作，不存在求導和函式連續性的限定；具有內在的隱並行性和更好的全局尋優能力；採用機率化的尋優方法，能自動獲取和指導最佳化的搜尋空間，自適應地調整搜尋方向，不需要確定的規則。遺傳算法的這些性質，已被人們廣泛地套用於組合最佳化、機器學習、信號處理、自適應控制和人工生命等領域。它是現代有關智慧型計算中的關鍵技術。

對於一個求函式最大值的最佳化問題（求函式最小值也類同），一般可以描述為下列數學規劃模型：

遺傳[生物進化過程的計算模型]

遺傳[生物進化過程的計算模型]

遺傳[生物進化過程的計算模型]

遺傳[生物進化過程的計算模型]

遺傳[生物進化過程的計算模型]

遺傳[生物進化過程的計算模型]

式中 為決策變數， 為 目標函式式， 、 為約束條件，U是基本空間，R是U的子集。滿足約束條件的解 稱為可行解，集合R表示所有滿足約束條件的解所組成的集合，稱為可行解集合。

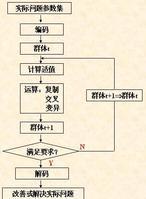
遺傳算法也是計算機科學人工智慧領域中用於解決最最佳化的一種搜尋啟發式算法，是進化算法的一種。這種啟發式通常用來生成有用的解決方案來最佳化和搜尋問題。進化算法最初是借鑑了進化生物學中的一些現象而發展起來的，這些現象包括遺傳、突變、自然選擇以及雜交等。遺傳算法在適應度函式選擇不當的情況下有可能收斂於局部最優 ，而不能達到全局最優。遺傳算法的基本運算過程如下：

a)初始化：設定進化代數計數器t=0，設定最大進化代數T，隨機生成M個個體作為初始群體P(0)。

b)個體評價：計算群體P(t)中各個個體的適應度。

c)選擇運算：將選擇運算元作用於群體。選擇的目的是把最佳化的個體直接遺傳到下一代或通過配對交叉產生新的個體再遺傳到下一代。選擇操作是建立在群體中個體的適應度評估基礎上的。

d)交叉運算：將交叉運算元作用於群體。遺傳算法中起核心作用的就是交叉運算元。

e)變異運算：將變異運算元作用於群體。即是對群體中的個體串的某些基因座上的基因值作變動。群體P(t)經過選擇、交叉、變異運算之後得到下一代群體P(t+1)。

f)終止條件判斷：若t=T,則以進化過程中所得到的具有最大適應度個體作為最優解輸出，終止計算。

特點

遺傳算法是解決搜尋問題的一種通用算法，對於各種通用問題都可以使用。搜尋算法的共同特徵為：

① 首先組成一組候選解

② 依據某些適應性條件測算這些候選解的適應度

③ 根據適應度保留某些候選解，放棄其他候選解

④ 對保留的候選解進行某些操作，生成新的候選解。

遺傳算法

在遺傳算法中，上述幾個特徵以一種特殊的方式組合在一起：基於染色體群的並行搜尋，帶有猜測性質的選擇操作、交換操作和突變操作。這種特殊的組合方式將遺傳算法與其它搜尋算法區別開來。

遺傳算法還具有以下幾方面的特點：

(1)遺傳算法從問題解的串集開始搜尋，而不是從單個解開始。這是遺傳算法與傳統最佳化算法的極大區別。傳統最佳化算法是從單個初始值疊代求最優解的；容易誤入局部最優解。遺傳算法從串集開始搜尋，覆蓋面大，利於全局擇優。

(2)遺傳算法同時處理群體中的多個個體，即對搜尋空間中的多個解進行評估，減少了陷入局部最優解的風險，同時算法本身易於實現並行化。

(3)遺傳算法基本上不用搜尋空間的知識或其它輔助信息，而僅用適應度函式值來評估個體，在此基礎上進行遺傳操作。適應度函式不僅不受連續可微的約束，而且其定義域可以任意設定。這一特點使得遺傳算法的套用範圍大大擴展。

(4)遺傳算法不是採用確定性規則，而是採用機率的變遷規則來指導他的搜尋方向。

(5)具有自組織、自適應和自學習性。遺傳算法利用進化過程獲得的信息自行組織搜尋時，適應度大的個體具有較高的生存機率，並獲得更適應環境的基因結構。

(6)此外，算法本身也可以採用動態自適應技術，在進化過程中自動調整算法控制參數和編碼精度，比如使用模糊自適應法 。

現狀

進入90年代，遺傳算法迎來了興盛發展時期，無論是理論研究還是套用研究都成了十分熱門的課題。尤其是遺傳算法的套用研究顯得格外活躍，不但它的套用領域擴大，而且利用遺傳算法進行最佳化和規則學習的能力也顯著提高，同時產業套用方面的研究也在摸索之中。此外一些新的理論和方法在套用研究中亦得到了迅速的發展，這些無疑均給遺傳算法增添了新的活力。遺傳算法的套用研究已從初期的組合最佳化求解擴展到了許多更新、更工程化的套用方面。

隨著套用領域的擴展，遺傳算法的研究出現了幾個引人注目的新動向：一是基於遺傳算法的機器學習，這一新的研究課題把遺傳算法從歷來離散的搜尋空間的最佳化搜尋算法擴展到具有獨特的規則生成功能的嶄新的機器學習算法。這一新的學習機制對於解決人工智慧中知識獲取和知識最佳化精煉的瓶頸難題帶來了希望。二是遺傳算法正日益和神經網路、模糊推理以及混沌理論等其它智慧型計算方法相互滲透和結合，這對開拓21世紀中新的智慧型計算技術將具有重要的意義。三是並行處理的遺傳算法的研究十分活躍。這一研究不僅對遺傳算法本身的發展，而且對於新一代智慧型計算機體系結構的研究都是十分重要的。四是遺傳算法和另一個稱為人工生命的嶄新研究領域正不斷滲透。所謂人工生命即是用計算機模擬自然界豐富多彩的生命現象，其中生物的自適應、進化和免疫等現象是人工生命的重要研究對象，而遺傳算法在這方面將會發揮一定的作用，五是遺傳算法和進化規劃（Evolution Programming,EP）以及進化策略（Evolution Strategy,ES）等進化計算理論日益結合。EP和ES幾乎是和遺傳算法同時獨立發展起來的，同遺傳算法一樣，它們也是模擬自然界生物進化機制的智慧型計算方法，即同遺傳算法具有相同之處，也有各自的特點。目前，這三者之間的比較研究和彼此結合的探討正形成熱點。

1991年D.Whitey在他的論文中提出了基於鄰域交叉的交叉運算元（Adjacency based crossover），這個運算元是特別針對用序號表示基因的個體的交叉，並將其套用到了TSP問題中，通過實驗對其進行了驗證。D.H.Ackley等提出了隨機疊代遺傳爬山法（Stochastic Iterated Genetic Hill-climbing，SIGH）採用了一種複雜的機率選舉機制，此機制中由m個“投票者”來共同決定新個體的值（m表示群體的大小）。實驗結果表明，SIGH與單點交叉、均勻交叉的神經遺傳算法相比，所測試的六個函式中有四個表現出更好的性能，而且總體來講，SIGH比現存的許多算法在求解速度方面更有競爭力。H.Bersini和G.Seront將遺傳算法與單一方法（simplex method）結合起來，形成了一種叫單一操作的多親交叉運算元（simplex crossover），該運算元在根據兩個母體以及一個額外的個體產生新個體，事實上他的交叉結果與對三個個體用選舉交叉產生的結果一致。同時，文獻還將三者交叉運算元與點交叉、均勻交叉做了比較，結果表明，三者交叉運算元比其餘兩個有更好的性能。

1992年，英國格拉斯哥大學的李耘（Yun Li）指導博士生將基於二進制基因的遺傳算法擴展到七進制、十進制、整數、浮點等的基因，以便將遺傳算法更有效地套用於模糊參量，系統結構等的直接最佳化，於1997年開發了可能是世界上最受歡迎的、也是最早之一的遺傳/進化算法的網上程式 EA_demo，以幫助新手線上互動式了解進化計算的編碼和工作原理 ，並在格拉斯哥召開第二屆IEE/IEEE遺傳算法套用國際會議，於2000年組織了由遺傳編程(Genetic Programming)發明人斯坦福的 John Koza 等參加的 EvoNet 研討會，探索融合GA與GP結構尋優，超越固定結構和數值最佳化的局限性。

國內也有不少的專家和學者對遺傳算法的交叉運算元進行改進。2002年，戴曉明等套用多種群遺傳並行進化的思想，對不同種群基於不同的遺傳策略，如變異機率，不同的變異運算元等來搜尋變數空間，並利用種群間遷移運算元來進行遺傳信息交流，以解決經典遺傳算法的收斂到局部最優值問題

2004年，趙宏立等針對簡單遺傳算法在較大規模組合最佳化問題上搜尋效率不高的現象，提出了一種用基因塊編碼的並行遺傳算法（Building-block Coded Parallel GA，BCPGA）。該方法以粗粒度並行遺傳算法為基本框架，在染色體群體中識別出可能的基因塊，然後用基因塊作為新的基因單位對染色體重新編碼，產生長度較短的染色體，在用重新編碼的染色體群體作為下一輪以相同方式演化的初始群體。

2005年，江雷等針對並行遺傳算法求解TSP問題，探討了使用彈性策略來維持群體的多樣性，使得算法跨過局部收斂的障礙，向全局最優解方向進化。

基本框架

編碼

遺傳算法不能直接處理問題空間的參數，必須把它們轉換成遺傳空間的由基因按一定結構組成的染色體或個體。這一轉換操作就叫做編碼，也可以稱作（問題的）表示（representation）。

遺傳算法

評估編碼策略常採用以下3個規範：

a)完備性(completeness):問題空間中的所有點(候選解)都能作為GA空間中的點(染色體)表現。

b)健全性(soundness): GA空間中的染色體能對應所有問題空間中的候選解。

c)非冗餘性(nonredundancy):染色體和候選解一一對應。

目前的幾種常用的編碼技術有二進制編碼，浮點數編碼，字元編碼，變成編碼等。

而二進制編碼是目前遺傳算法中最常用的編碼方法。即是由二進制字元集{0,1}產生通常的0,1字元串來表示問題空間的候選解。它具有以下特點：

a)簡單易行

b)符合最小字元集編碼原則

c)便於用模式定理進行分析，因為模式定理就是以基礎的。

適應度函式

進化論中的適應度，是表示某一個體對環境的適應能力，也表示該個體繁殖後代的能力。遺傳算法的適應度函式也叫評價函式，是用來判斷群體中的個體的優劣程度的指標，它是根據所求問題的目標函式來進行評估的。

遺傳算法在搜尋進化過程中一般不需要其他外部信息，僅用評估函式來評估個體或解的優劣，並作為以後遺傳操作的依據。由於遺傳算法中，適應度函式要比較排序並在此基礎上計算選擇機率，所以適應度函式的值要取正值。由此可見，在不少場合，將目標函式映射成求最大值形式且函式值非負的適應度函式是必要的。

適應度函式的設計主要滿足以下條件：

a）單值、連續、非負、最大化

b) 合理、一致性

c）計算量小

d）通用性強。

在具體套用中，適應度函式的設計要結合求解問題本身的要求而定。適應度函式設計直接影響到遺傳算法的性能。

初始群體選取

遺傳算法中初始群體中的個體是隨機產生的。一般來講，初始群體的設定可採取如下的策略:

a)根據問題固有知識，設法把握最優解所占空間在整個問題空間中的分布範圍，然後，在此分布範圍內設定初始群體。

b)先隨機生成一定數目的個體，然後從中挑出最好的個體加到初始群體中。這種過程不斷疊代，直到初始群體中個體數達到了預先確定的規模。

一般算法

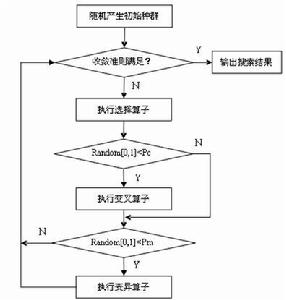
遺傳算法是基於生物學的，理解或編程都不太難。下面是遺傳算法的一般算法：

建初始狀態

初始種群是從解中隨機選擇出來的，將這些解比喻為染色體或基因，該種群被稱為第一代，這和符號人工智慧系統的情況不一樣，在那裡問題的初始狀態已經給定了。

評估適應度

對每一個解(染色體)指定一個適應度的值，根據問題求解的實際接近程度來指定(以便逼近求解問題的答案)。不要把這些“解”與問題的“答案”混為一談，可以把它理解成為要得到答案，系統可能需要利用的那些特性。

繁殖

繁殖(包括子代突變)

帶有較高適應度值的那些染色體更可能產生後代(後代產生後也將發生突變)。後代是父母的產物，他們由來自父母的基因結合而成，這個過程被稱為“雜交”。

下一代

如果新的一代包含一個解，能產生一個充分接近或等於期望答案的輸出，那么問題就已經解決了。如果情況並非如此，新的一代將重複他們父母所進行的繁衍過程，一代一代演化下去，直到達到期望的解為止。

並行計算

非常容易將遺傳算法用到並行計算和群集環境中。一種方法是直接把每個節點當成一個並行的種群看待。然後有機體根據不同的繁殖方法從一個節點遷移到另一個節點。另一種方法是“農場主/勞工”體系結構，指定一個節點為“農場主”節點，負責選擇有機體和分派適應度的值，另外的節點作為“勞工”節點，負責重新組合、變異和適應度函式的評估。

術語說明

由於遺傳算法是由進化論和遺傳學機理而產生的搜尋算法，所以在這個算法中會用到很多生物遺傳學知識，下面是我們將會用來的一些術語說明：

染色體

染色體又可以叫做基因型個體(individuals),一定數量的個體組成了群體(population),群體中個體的數量叫做群體大小。

基因

基因是串中的元素，基因用於表示個體的特徵。例如有一個串S=1011，則其中的1，0，1，1這4個元素分別稱為基因。它們的值稱為等位基因(Alleles)。

基因位點

基因位點在算法中表示一個基因在串中的位置稱為基因位置(Gene Position)，有時也簡稱基因位。基因位置由串的左向右計算，例如在串 S=1101 中，0的基因位置是3。

特徵值

在用串表示整數時，基因的特徵值與二進制數的權一致；例如在串 S=1011 中，基因位置3中的1，它的基因特徵值為2；基因位置1中的1，它的基因特徵值為8。

適應度

各個個體對環境的適應程度叫做適應度(fitness)。為了體現染色體的適應能力，引入了對問題中的每一個染色體都能進行度量的函式，叫適應度函式。 這個函式是計算個體在群體中被使用的機率。

運算過程

遺傳過程

遺傳操作是模擬生物基因遺傳的做法。在遺傳算法中，通過編碼組成初始群體後，遺傳操作的任務就是對群體的個體按照它們對環境適應度(適應度評估)施加一定的操作，從而實現優勝劣汰的進化過程。從最佳化搜尋的角度而言，遺傳操作可使問題 的解，一代又一代地最佳化，並逼近最優解。

遺傳操作包括以下三個基本遺傳運算元(genetic operator):選擇(selection)；交叉(crossover)；變異(mutation)。這三個遺傳運算元有如下特點：

個體遺傳運算元的操作都是在隨機擾動情況下進行的。因此，群體中個體向最優解遷移的規則是隨機的。需要強調的是，這種隨機化操作和傳統的隨機搜尋方法是有區別的。遺傳操作進行的高效有向的搜尋而不是如一般隨機搜尋方法所進行的無向搜尋。

遺傳操作的效果和上述三個遺傳運算元所取的操作機率，編碼方法，群體大小，初始群體以及適應度函式的設定密切相關。

選擇

遺傳算法

從群體中選擇優勝的個體，淘汰劣質個體的操作叫選擇。選擇運算元有時又稱為再生運算元(reproduction operator)。選擇的目的是把最佳化的個體(或解)直接遺傳到下一代或通過配對交叉產生新的個體再遺傳到下一代。選擇操作是建立在群體中個體的適應度評估基礎上的，目前常用的選擇運算元有以 下幾種：適應度比例方法、隨機遍歷抽樣法、局部選擇法。

其中輪盤賭選擇法 （roulette wheel selection）是最簡單也是最常用的選擇方法。在該方法中，各個個體的選擇機率和其適應度值成比例。設群體大小為n，其中個體i的適應度為，則i 被選擇的機率，為遺傳算法

顯然，機率反映了個體i的適應度在整個群體的個體適應度總和中所占的比例。個體適應度越大。其被選擇的機率就越高、反之亦然。計算出群體中各個個體的選擇機率後，為了選擇交配個體，需要進行多輪選擇。每一輪產生一個[0，1]之間均勻隨機數，將該隨機數作為選擇指針來確定被選個體。個體被選後，可隨機地組成交配對，以供後面的交叉操作。

交叉

在自然界生物進化過程中起核心作用的是生物遺傳基因的重組(加上變異)。同樣，遺傳算法中起核心作用的是遺傳操作的交叉運算元。所謂交叉是指把兩個父代個體的部分結構加以替換重組而生成新個體的操作。通過交叉，遺傳算法的搜尋能力得以飛躍提高。

交叉運算元根據交叉率將種群中的兩個個體隨機地交換某些基因，能夠產生新的基因組合，期望將有益基因組合在一起。根據編碼表示方法的不同，可以有以下的算法：

a)實值重組（real valued recombination）

1)離散重組（discrete recombination）

2)中間重組（intermediate recombination）

3)線性重組（linear recombination）

4)擴展線性重組（extended linear recombination）。

b)二進制交叉（binary valued crossover）

1)單點交叉（single-point crossover）

2)多點交叉（multiple-point crossover）

3)均勻交叉（uniform crossover）

4)洗牌交叉（shuffle crossover）

5)縮小代理交叉（crossover with reduced surrogate）。

最常用的交叉運算元為單點交叉(one-point crossover)。具體操作是:在個體串中隨機設定一個交叉點，實行交叉時，該點前或後的兩個個體的部分結構進行互換，並生成兩個新個體。下面給出了單點交叉的一個例子：

個體A：1 0 0 1 ↑1 1 1 → 1 0 0 1 0 0 0 新個體

個體B：0 0 1 1 ↑0 0 0 → 0 0 1 1 1 1 1 新個體

變異

變異運算元的基本內容是對群體中的個體串的某些基因座上的基因值作變動。依據個體編碼表示方法的不同，可以有以下的算法：

a)實值變異

b)二進制變異。

一般來說，變異運算元操作的基本步驟如下：

a)對群中所有個體以事先設定的變異機率判斷是否進行變異

b)對進行變異的個體隨機選擇變異位進行變異。

遺傳算法引入變異的目的有兩個:一是使遺傳算法具有局部的隨機搜尋能力。當遺傳算法通過交叉運算元已接近最優解鄰域時，利用變異運算元的這種局部隨機搜尋能力可以加速向最優解收斂。顯然，此種情況下的變異機率應取較小值，否則接近最優解的積木塊會因變異而遭到破壞。二是使遺傳算法可維持群體多樣性，以防止出現未成熟收斂現象。此時收斂機率應取較大值。

遺傳算法中，交叉運算元因其全局搜尋能力而作為主要運算元，變異運算元因其局部搜尋能力而作為輔助運算元。遺傳算法通過交叉和變異這對相互配合又相互競爭的操作而使其具備兼顧全局和局部的均衡搜尋能力。所謂相互配合.是指當群體在進化中陷於搜尋空間中某個超平面而僅靠交叉不能擺脫時，通過變異操作可有助於這種擺脫。所謂相互競爭，是指當通過交叉已形成所期望的積木塊時，變異操作有可能破壞這些積木塊。如何有效地配合使用交叉和變異操作，是目前遺傳算法的一個重要研究內容。

基本變異運算元是指對群體中的個體碼串隨機挑選一個或多個基因座並對這些基因座的基因值做變動(以變異機率P.做變動)，(0，1)二值碼串中的基本變異操作如下：

基因位下方標有*號的基因發生變異。

遺傳算法

變異率的選取一般受種群大小、染色體長度等因素的影響，通常選取很小 的值，一般取0.001－0.1。

終止條件

當最優個體的適應度達到給定的閾值，或者最優個體的適應度和群體適應度不再上升時，或者疊代次數達到預設的代數時，算法終止。預設的代數一般設定為100-500代。

不足之處

(1)編碼不規範及編碼存在表示的不準確性。

(2)單一的遺傳算法編碼不能全面地將最佳化問題的約束表示出來。考慮約束的一個方法就是對不可行解採用閾值，這樣，計算的時間必然增加。

(3)遺傳算法通常的效率比其他傳統的最佳化方法低。

(4)遺傳算法容易過早收斂。

(5)遺傳算法對算法的精度、可行度、計算複雜性等方面，還沒有有效的定量分析方法。

套用

由於遺傳算法的整體搜尋策略和最佳化搜尋方法在計算時不依賴於梯度信息或其它輔助知識，而只需要影響搜尋方向的目標函式和相應的適應度函式，所以遺傳算法提供了一種求解複雜系統問題的通用框架，它不依賴於問題的具體領域，對問題的種類有很強的魯棒性，所以廣泛套用於許多科學，下面我們將介紹遺傳算法的一些主要套用領域：

函式最佳化

函式最佳化是遺傳算法的經典套用領域，也是遺傳算法進行性能評價的常用算例，許多人構造出了各種各樣複雜形式的測試函式：連續函式和離散函式、凸函式和凹函式、低維函式和高維函式、單峰函式和多峰函式等。對於一些非線性、多模型、多目標的函式最佳化問題，用其它最佳化方法較難求解，而遺傳算法可以方便的得到較好的結果。

組合最佳化

隨著問題規模的增大，組合最佳化問題的搜尋空間也急劇增大，有時在目前的計算上用枚舉法很難求出最優解。對這類複雜的問題，人們已經意識到應把主要精力放在尋求滿意解上，而遺傳算法是尋求這種滿意解的最佳工具之一。實踐證明，遺傳算法對於組合最佳化中的NP問題非常有效。例如遺傳算法已經在求解旅行商問題、 背包問題、裝箱問題、圖形劃分問題等方面得到成功的套用。

此外，GA也在生產調度問題、自動控制、機器人學、圖象處理、人工生命、遺傳編碼和機器學習等方面獲得了廣泛的運用。

車間調度

車間調度問題是一個典型的NP-Hard問題，遺傳算法作為一種經典的智慧型算法廣泛用於車間調度中，很多學者都致力於用遺傳算法解決車間調度問題，現今也取得了十分豐碩的成果。從最初的傳統車間調度（JSP）問題到柔性作業車間調度問題（FJSP），遺傳算法都有優異的表現，在很多算例中都得到了最優或近優解。

演示學習

EA_demo，英國格拉斯哥大學1997年出版 ，至今仍廣泛使用，採用大學包括英國利物浦（Liverpool）大學、蘇塞克斯（Sussex）大學、北安普頓（Northampton）大學，德國烏爾姆（Ulm）大學，瑞士日內瓦（Geneva）大學，西班牙格瑞那達（Granada）大學，葡萄牙新里斯本（Nova de Lisboa）大學，美國加州大學戴維斯分校（UC Davies），加拿大卡爾加里（Calgary）大學，澳大利亞墨爾本皇家理工大學（RMIT），新加坡國立大學，台灣國立清華大學，上海交通大學，巴西PUCRS大學等。

EA_demo允許用戶直接在網頁上一代一代地手動運行，以看遺傳/進化算法是怎樣一步一步操作的，亦可在背景中批次運行，以觀察算法的收斂和染色體是否跳出局部最優。用戶可以改變終止代數，群體規模，交配率，變異率和選擇機制。也有其它自學課件收錄於AI中心網站和歐洲軟計算中心網站。