簡介
運算元方法是用以求解常係數線性高階常微分方程特解的一種簡便方法。
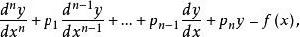 運算元方法
運算元方法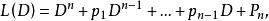 運算元方法
運算元方法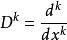 運算元方法
運算元方法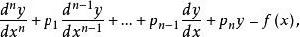 運算元方法
運算元方法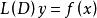 運算元方法
運算元方法對於常係數線性常微分方程 引入運算元 其中D=d/dx表示對x求微商的運算, 表示對x求k次微商。L(D)稱為運算元多項式。方程 可簡寫為 。
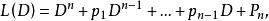 運算元方法
運算元方法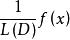 運算元方法
運算元方法根據 記 為方程的任一解,稱1/L(D)為L(D)的逆運算元。
套用
運用運算元L(D)和逆運算元1/L(D)的性質和法則可以簡便地求解方程。特別當n≥3,f(x)為x ,e ,cosβx,sinβx等類函式之和,或它們乘積之和時,求方程的特解較用常數變易法簡便。
運算元方法類似地可運用到常係數線性常微分方程組中去。
運算元
運算元是一個函式空間到函式空間上的映射O:X→X。
廣義上的運算元可以推廣到任何空間,如內積空間等。對任何函式進行某一項操作都可以認為是一個運算元,甚至包括求冪次,開方都可以認為是一個運算元,只是有的運算元我們用了一個符號來代替他所要進行的運算。
