簡介
變速圓周運動（英語：Non-uniform circular motion）是圓周運動的一種，指的是物體移動的角速度隨著時間變化的圓周運動。正在做變速圓周運動的物體，其各個位置向心加速度之和不等於零，切向加速度也不為零。
如果一個物體正在做變速圓周運動，則說明有外力正在改變圓周運動的性質，這個力可以是重力、正向力或摩擦力。生活中大部分的圓周（離心）運動，都存在切向的加速度，即為變速圓周運動。
變速圓周運動
變速圓周運動在變速圓周運動的過程中，正向力和重力不在同一條直線上。過山車旋轉一周的過程就是變速圓周運動，在底部速度最快，頂端速度最慢。重力是這個過程中阻礙過山車做勻速圓周運動的主要因素。
受力分析
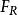變速圓周運動
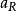變速圓周運動
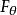變速圓周運動
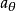變速圓周運動物體在做勻速圓周運動時，其所受的合力（向心力）永遠指向圓心。但是在變速圓周運動的過程中，物體所受合力指向圓心的分量產生向心加速度，使物體保持圓周移動。其相切分量則改變線速度的大小，因而產生一個圓周的切線加速度分量，其大小為：
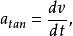變速圓周運動而向心加速度是由速度方向的變化所產生的，其大小和物體做勻速圓周運動時一樣，為：
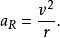變速圓周運動
變速圓周運動此時物體總加速度的矢量等於這兩個分量之和：
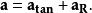變速圓周運動豎直平面內的變速圓周運動
繩球模型
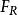變速圓周運動 變速圓周運動
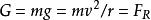變速圓周運動沒有其他物體支持的物體在豎直平面內做圓周運動時（例如一個物體綁在繩子上做圓周運動），其能夠完成一個圓周運動的臨界條件為在物體通過圓周最頂端的時候，其受到的重力剛好充當了圓周運動的向心力，即，由此得到物體通過最高點的最小的速度為：
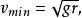變速圓周運動其中：g為重力加速度，r為圓周運動的半徑。
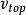變速圓周運動
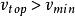變速圓周運動
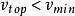變速圓周運動假設物體通過圓周最頂端的速度為，當時，物體能夠完成圓周運動。當時，物體在達到頂端之前就開始做斜拋運動。
桿球模型
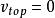變速圓周運動 變速圓周運動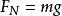
變速圓周運動有其他物體支持的物體在豎直平面內做圓周運動時（例如一個物體綁在輕桿上做圓周運動），由於有其他物體（輕桿）支撐，物體在頂端的最小速度為零，即。此時物體收到的力分別為重力和（輕桿的）支持力。
