簡介
流動理論假設材料的徐變與粘滯流動具有某種相似的性質,認為徐變的應變速率與應力、時間之間存在著某種簡單的函式關係,即:
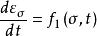 流動理論
流動理論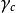 流動理論
流動理論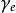 流動理論
流動理論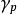 流動理論
流動理論以、 和 表示徐變應變速率、彈性應變速率和塑性應變速率,由此得到總的應變速率為:
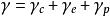 流動理論
流動理論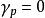 流動理論
流動理論當應力未超過彈性極限時,,彈性應變速率為:
 流動理論
流動理論試驗發現,當工作溫度不變時,金屬材料在緩慢並單調變化的應力作用下,徐變的應變速率可表示為:
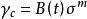 流動理論
流動理論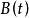 流動理論
流動理論式中,等於單位應力作用下的徐變速率。
由此可得總應變速率為:
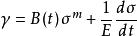 流動理論
流動理論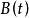 流動理論
流動理論在上式中,當為常數且m=1時,可得到Maxwell方程,故流動理論方程是Maxwell方程的普遍形式。
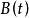 流動理論
流動理論當時間很長時,接近於常數B,如果載荷不變且可以略去微小的彈性應變速率,則採用更為簡單的流動理論規律:
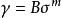 流動理論
流動理論這一方程描述了物體非線性粘滯流動的性質。
套用範圍與特點
流動理論在套用上具有與老化理論相似的限制:在應力為單調而且緩慢變化的情況下,流動理論是適用的 。流動理論方程明顯地包含時間因素,起始時刻若有變化,則流動理論的方程也相應變化。
流動理論與形變理論
流動理論與形變理論之間存在一定的關係。在簡單載入條件下,從流動理論可以導出形變理論,簡單載入下形變理論與流動理論是一致的。在載入路徑偏離簡單載入不大時,由形變理論得到的結果也與流動理論相差不多。

