樹狀結構定義
它滿足:
 樹狀結構
樹狀結構n有一個特定的點稱為根節點(root),
n其餘的節點分成n³0個獨立的集合T1, …, Tn,每個集合也都是一個樹狀結構。我們講T1, …, Tn為根節點的子樹(subtree)。
節點與邊:節點代表某項資料,而邊是指由一節點到另一節點的分支。
祖先(ancestor)即點與子孫(descendant)節點:如圖,A是所有節點的祖先,所有節點是A的子孫;而F是K與L的祖先,K與L是F的子孫。
父節點(parent node)與子節點(children node):如圖,B直接連到E與F且只差一個階度,則B為E與F的父節點,E與F為B的子節點。
兄弟節點(sibling node):擁有同一父節點的子節點。如:E與F。
葉節點(leaf node)或終點節點(terminal node):沒有子節點的節點。如:J、K等。
非葉節點(non-leaf node)或非終點節點(non-terminal node):有子節點的節點。 如:A、B、F等等。
根節點(root node):沒有父節點的節點,為樹的源頭。 如:A。
分支度(degree):指一個節點有幾個子節點。 如:A為3、B為2、C為1、M為0。
階度(level):為樹中的第幾代,而根節點為第一代,階度為1。
高度(height):指一節點往下走到葉節點的最長路徑。 如:A為3、F為1、L為0。
深度(depth):指從根節點到某一節點的最長路徑。如:C為1、M為3。
樹林(forest):由多個互斥樹(disjoint tree)所組成。 如圖將A移去便成為樹林。
二元樹(Binarytree)
 樹狀結構
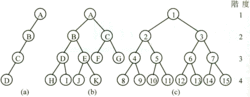
樹狀結構二元樹(Binary tree):二元樹里每一節點的最大分支度為2。 如下右(a)、(b)、(c)。
圖(a)稱做左斜樹(left skew tree),每一節點的右子樹皆為空集合。
圖(c)稱為滿枝二元樹(fully binary tree),含有節點數共為2k-1。
圖(b)稱為完整二元樹(complete binary tree),節點排列順序同滿枝二元樹,但節點數小於2k-1 。
二元哪種的第i階最多有2i-1個節點。
如果有一n個節點的完整二元樹,以循序的方式編號,如上圖(c)。 則任何一個節點i,1 ≤ i ≤ n,具有以下的特性:
若i = 1,則i為根節點,沒有父節點。 而i ≠ 1,其父節點為ëi/2û(表小於i/2的最大整數)。
若2i ≤ n,則i的左子節點在2i。 但若2i > n,則i沒有左子節點。
若2i+1 ≤ n,則i的右子節點在2i+1。 但若2i+1 > n,則i沒有右子節點。
節點i在第[log2 ]+1階。
