概念
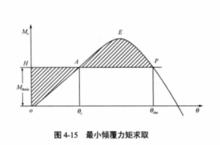 圖1
圖1在靜穩性曲線圖上,外力矩曲線下面積與穩性力矩曲線下面積相等時對應的橫傾角即為動傾角。由作圖求θ可知,當外力矩M增大時,M曲線位置提高,曲線下的面積增大。為取得動平衡,需有更多的M曲線面積抵償,則計算曲線面積時的右邊界線後移,相應的動傾角增大。如圖1所示,當外力矩M增大到某一數值時,曲線圖中坐標縱軸、M曲線及M直線所包圍的面積OHA等於M直線與M曲線所圍冠狀面積AEP,使得船舶動平衡達到極限位置。若將M值再增大時,則無論橫傾角多大,M曲線下的面積恆大於M曲線下的面積,船舶不再滿足動平衡條件,也就不存在動平衡位置。
顯而易見,從動穩性角度分析,船舶在極限動平衡時對應的外力矩為船舶能夠承受外力矩的最大能力;或者說,該外力矩是使船舶傾覆所需要的最小值。當實際外力矩大於該值時,船舶因動平衡不復存在而導致傾覆。因此,將船舶在極限動平衡時的外力矩稱為最小傾復力矩,以M。表示。它是衡量船舶動穩性的重要參數。船舶在最小傾覆力矩作用下所對應的動傾角稱為極限動傾角,以θ表示。
從動穩性要求來考慮,保證船舶不致傾覆的條件應為
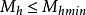 最小傾復力矩
最小傾復力矩動穩性曲線圖
 最小傾復力矩
最小傾復力矩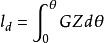 最小傾復力矩
最小傾復力矩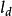 最小傾復力矩
最小傾復力矩描述船舶自正浮位置橫傾至任一傾角時復原力矩做功的曲線稱為動穩性曲線,由 可知,動穩性圖描述的是0~θ角之間復原力矩(臂)曲線與θ軸所圍的面積,可通過近似積分法求得。動穩性曲線也可用復原力臂的積分曲線 來描述, 稱為動復原力臂。
動穩性圖的套用
求取動平衡角
 圖2
圖2 最小傾復力矩
最小傾復力矩 最小傾復力矩
最小傾復力矩當橫傾力矩M=C時,橫傾力矩做功曲線 是一過原點O且斜率為M的直線 ,當0為1 rad(57.3°)時,W與M的數值相等。
如圖2所示,MN=M,W曲線和W直線的交點E滿足動平衡條件W=W,該點所對應的角即為動平衡角。
求最小傾覆力矩
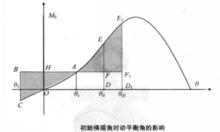 圖3
圖3過原點O作動穩性曲線的切線,切點為F。該切線的斜率MP為最小傾覆力矩M,如圖2所示。
 最小傾復力矩
最小傾復力矩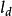 最小傾復力矩
最小傾復力矩 最小傾復力矩
最小傾復力矩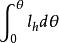 最小傾復力矩
最小傾復力矩利用動穩性圖來確定θ和M較為簡單、直觀。如果利用動復原力臂 曲線來圖解動平衡θ和最小傾覆力臂 時,橫傾力矩做功曲線 應被橫傾力臂積分曲線 替代。
最小傾覆力矩的影響因素
風浪聯合作用
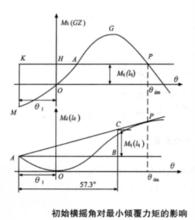 圖4
圖4 最小傾復力矩
最小傾復力矩 最小傾復力矩
最小傾復力矩 最小傾復力矩
最小傾復力矩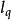 最小傾復力矩
最小傾復力矩船舶受到波浪作用發生搖擺,當船舶向迎風一舷橫搖至角θ,剛要回橫搖時,如圖3所示,船舶受到突風作用,此時復原力矩與橫傾力矩同向,二者共同使船舶加速回搖,船舶動平衡角由不考慮初始橫搖角時的θ增加到θ。這種風、浪疊加(風浪聯合)作用( Joint action of wind and wave)成為船舶穩性在波浪運動中最不利的情況。在確定最小傾覆力矩 (力臂 )時也應計入初始橫搖角θ的影響,如圖4所示,在靜穩性曲線圖中,滿足面積KAM與面積AGP相等時,線段OA值即為最小傾覆力矩(力臂)。在動穩性曲線圖中,自原點沿θ軸上向θ負值方向對應延伸,取等於所算得的橫搖角θ的一點,經此點向上作θ軸的垂直線,與動穩性曲線交於A點,由A點作動穩性曲線的切線,再經A點作一直線平行於θ軸,自A點起,在此直線上量取等於1 rad( 57.3°)的一段長度得B點,由B點向上作AB線的垂直線,與上述的切線相交於C點,則線段BC為最小傾覆力矩(力臂)。
進水角
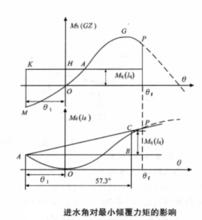 圖5
圖5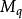 最小傾復力矩
最小傾復力矩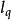 最小傾復力矩
最小傾復力矩進水角θ( Angel of flooding)是指船舶橫傾至非水密開口時的橫傾角。肖船舶橫傾至進水角時,船舶穩性喪失。在穩性圖上(圖5),當θ<θ時,θ以後的曲線面積不再計入。當動穩性曲線因進水角θ影響而中斷時,在確定最小傾覆力矩(力臂)時,除了由A點作動穩性曲線的切線用經過動穩性曲線中斷處的割線代替外,其餘原理均相同,最小傾覆力矩將因為進水角而減小。
傾覆試驗
海洋工程結構物在風浪中的傾覆是十分複雜的問題,其主要困難在於隨機外載荷的確定和大幅度橫搖的非線性性質。海洋結構物在橫浪情況下的大幅度橫搖以及在隨浪狀況下,由於遭遇周期性波浪而產生的、隨時間周期性變化的回覆力矩引起的參數共振是傾覆的主要原因。目前,海洋工程結構物的傾覆機理還沒有完全解決,因此,模型試驗是研究傾覆的可靠手段。
試驗的主要目的是研究海洋結構物在風浪環境中的安全性,確定結構物最小傾覆力矩和橫傾角。
海洋工程結構物在風浪中的傾斜過程,將同時受到風傾力矩、回復力矩、慣性力矩和阻尼力矩的聯合作用。因此,傾覆試驗中,模型與實船應滿足的相似條件除幾何相似、質量分布相似等以外,還應滿足阻尼力矩相似、風壓力矩相似等條件。
傾覆試驗應選取海洋結構物作業海域的極端海況為模型試驗的環境條件。風浪條件應包括迎浪、橫浪和隨浪等多種浪向。由於在不規則波浪中結構物傾覆發生的時問是隨機的,因此模型試驗所持續的時間要足夠長。
雖然實際波浪都是隨機的,但一列持續時間較長,可能導致共振的規則波列對於海洋結構物來說也是非常危險的。因此傾覆試驗還應包括模型在規則波中的工況。
傾覆試驗過程中,應對結構物的六自由度運動特別是橫搖運動、系泊系統受力等進行測量和記錄,以獲得傾覆時的橫搖角度等動力回響數據,進而得到結構物傾覆時的最小傾覆力矩,確定海洋結構物在風浪環境中橫搖運動等的穩定區域、臨界狀態等。

