1,n 個球有區別,m 個盒子有區別,允許有空盒,n≥m≥1
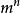 放球問題
放球問題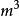 放球問題
放球問題由於可以有空盒,所以每個球可以放到m個盒子的任意一個盒子裡。又因為盒子是有區別的,所以對於任意一個球有m種不同的選擇。 n個球是有區別的,所以總共有 種方案。比如,當n=3 時,第 1 個球有m種不同選擇,第 2 個球有m種不同選擇,第3個球有m種不同選擇,據乘法法則總共有 種方案。
2. n 個球有區別,m 個盒子有區別,允許有空盒,m>n≥1。
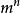 放球問題
放球問題由於可以有空盒,所以每個球可以放到m個盒子的任意一個盒子裡。又因為盒子是有區別的,所以對於任意一個球有m種不同的選擇。n個球是有區別的,所以總共有 種方案。
3. n 個球有區別,m 個盒子無區別,無空盒,n≥m≥1
根據中第二類司特林數的定義,n個有區別的球放到m個相同的盒子中,要求無一空盒,其不同的方案數為S(n,m)。
4. n 個球有區別,m 個盒子無區別,無空盒,m>n≥1
由於m>n,而n個球至多可放入n個盒子裡,所以必定有空盒。故滿足此條件的方案數為 0。
5. n 個球有區別,m 個盒子有區別,無空盒,n≥m≥1
對於這個問題,可以先假設m個盒子是無區別的,這樣根據 3 可知總共有S(n,m)種不同的方案數。然後再把m個盒子進行全排列,所以總共有m!S(n,m)種方案。
6. n 個球有區別,m 個盒子有區別,無空盒,m>n≥1
由於m>n, 而n個球至多可放入n個盒子裡,所以必定有空盒。故滿足此條件的方案數為 0。
7. n 個球有區別,m 個盒子無區別,允許有空盒,n≥m≥1
因為允許有空盒,我們可以設非空的盒子數是k個。則問題變成n個有區別的球放到k個無區別的盒子裡,要求無一空盒。據3可知,總共有S(n,k) 種方案。因為n≥m, k的取值範圍是[1, m], 所以共有S(n, 1) + S(n, 2) + …… + S(n, m)種方案。
8. n 個球有區別,m 個盒子無區別,允許有空盒,m>n≥1
因為允許有空盒,我們可以設非空的盒子數是k個。則問題變成n個有區別的球放到k個無區別的盒子裡,要求無一空盒。據3可知,總共有S(n,k) 種方案。因為m>n, k的取值範圍是[1, n], 所以共有S(n, 1) + S(n, 2) + …… + S(n, n)種方案。
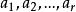 放球問題
放球問題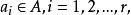 放球問題
放球問題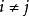 放球問題
放球問題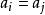 放球問題
放球問題9. n 個球無區別,m 個盒子有區別,允許有空盒,n≥m≥1
先介紹允許重複的組合的概念。允許重複的組合是指從集合A={1,2,……,n}中取r個元素{
也可利用“插板法”來理解。假設n個球和m-1個板放到n+m-1個位置,第1個板前的放進第一個盒子,第i-1個版和第i個版之間的球放進第i個盒子,則共有C(m+n-1,n)种放法。由於此時板可以連續放,故對應允許有空盒的情況。
10. n 個球無區別,m 個盒子有區別,允許有空盒,m>n≥1
此問題可表示為從m個不同的元素中取n個作允許重複的組合,其方案數為C(m+n-1, n)。
11. n 個球無區別,m 個盒子有區別,無空盒,n≥m≥1
由於要求無空盒,而且n個球無區別,所以先取出m個球放入m個盒子裡。此時,這個問題可轉化為求將(n-m)個無區別的球放入m個有區別的盒子裡,允許有空盒的方案數。這 個 問 題 就 變 成 了 9 所 解 決 的 問 題 。 因此有C(m+(n-m)-1, n-m)=C(n-1, n-m)=C(n-1, n-1-(n-m))=C(n-1,m-1)種方案。
 放球問題
放球問題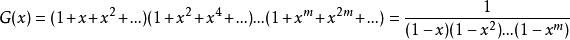 放球問題
放球問題12. n 個球無區別,m 個盒子有區別,無空盒,m>n≥1
由於n<m,而n個球至多可放入n個盒子裡,所以必定有空盒。故滿足此條件的方案數為 0。
13. n 個球無區別,m 個盒子無區別,允許有空盒,n≥m≥1
此問題相當於把n個球分成k堆,其中m>=k>1。根據中2.9 節的推論:設n≥m,n拆分成最多m個數的和的拆分數等於將n拆分成最大數不超過m的拆分數。據上述推論可把問題轉化為把整數n拆分成最大數不超過m的拆分數。而把整數拆分成最大不超過m的拆分數
 放球問題
放球問題故滿足條件的方案數等於把n用{1,2,...,m}進行拆分的拆分數,等於G(x)的
項係數。14. n 個球無區別,m 個盒子無區別,允許有空盒,m>n≥1
此問題相當於把n個球分成k堆。其中m>=k>1且n>=k>1。又因m>n,所以k的取值範圍為n>=k>1。
據13 可知此問題可轉化為把整數n拆分成最大數不超過n的拆分數。而把整數拆分成 最 大不 超 過n的 拆 分 數的母函式為
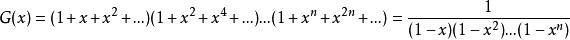 放球問題
放球問題 放球問題
放球問題故滿足條件的方案數等於把n用{1,2,...,n}進行拆分的拆分數,等於G(x)的 項係數。
15. n 個球無區別,m 個盒子無區別,無空盒,n≥m≥1
我們可先將每個盒子放一個球,然後利用類比13題,即
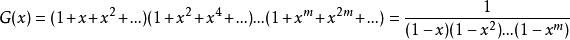 放球問題
放球問題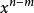 放球問題
放球問題滿足條件的方案數等於G(x)的 項係數。
16. n 個球無區別,m 個盒子無區別,無空盒,m>n≥1
由於n<m, 而n個球至多可放入n個盒子裡,所以必定有空盒。故滿足此條件的方案數為0。
| n個球是否有區別 | m個盒是否有區別 | 是否允許空盒 | n是否大於m | 方案數 | 簡要解釋 |
| 是 | 是 | 是 | 是 | 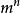 放球問題 放球問題 | 每個球有m種可能 |
| 否 | 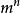 放球問題 放球問題 | 每個球有m種可能 | |||
| 否 | 是 | 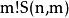 放球問題 放球問題 | 類比盒無區別時,再乘以盒的可能排列 | ||
| 否 | 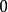 放球問題 放球問題 | 盒比球多,必有空盒 | |||
| 否 | 是 | 是 | 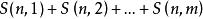 放球問題 放球問題 | 枚舉有球盒的數量,再利用斯特林數 | |
| 否 | 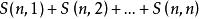 放球問題 放球問題 | 枚舉有球盒的數量,再利用斯特林數 | |||
| 否 | 是 | 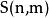 放球問題 放球問題 | 根據斯特林數定義 | ||
| 否 | 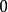 放球問題 放球問題 | 盒比球多,必有空盒 | |||
| 否 | 是 | 是 | 是 | 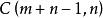 放球問題 放球問題 | 插板法或根據可重組合計算公式 |
| 否 | 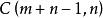 放球問題 放球問題 | 同上 | |||
| 否 | 是 | 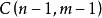 放球問題 放球問題 | 先給每盒放一球,然後利用n-m個球,m個盒子有空盒的解 | ||
| 否 | 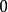 放球問題 放球問題 | 盒比球多,必有空盒 | |||
| 否 | 是 | 是 | 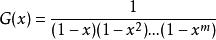 放球問題 放球問題  放球問題 放球問題 | 母函式方法 | |
| 否 | 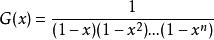 放球問題 放球問題  放球問題 放球問題 | 母函式方法 | |||
| 否 | 是 | 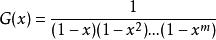 放球問題 放球問題 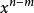 放球問題 放球問題 | 母函式方法 | ||
| 否 | 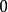 放球問題 放球問題 | 盒比球多,必有空盒 |
