拋物變換

簡介

分式線性變換

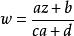拋物變換

分式線性變換是一種特殊的映射。從擴充z平面到擴充w平面到共形映射稱為分式線性變換，簡稱線性變換，即，其中a，b，c，d都是復常數，ad-bc≠0並且當z=∞時對應w=a/c，z=-d/c時對應w=∞。

分式線性變換總可以分解成下述簡單類型變換的複合：

1、w=kz+h(k≠0)；

2、w=1/z；

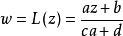拋物變換

拋物變換

除恆等變換w=z外，一個分式線性變換至多有兩個不動點（即在分式線性變換下映為自身的點），若L(z)僅有一個不動點，則稱L(z)為拋物變換。

判定

分式線性變換的不動點由下面的方程

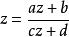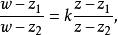拋物變換

拋物變換

決定，即cz+(d-a)z-b=0。若此二次方程有兩個不同的有窮根z，z，則變換L(z)可寫成其中k是常數。