定義
德卡斯特里奧算法貝茲曲線B（角度為n，控制點 ）可用以下方式運用德卡斯特里奧算法：
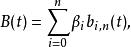德卡斯特里奧算法其中，b為伯恩施坦基本多項式。
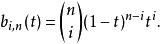德卡斯特里奧算法曲線在t0點上可以用遞推關係式運算。
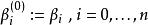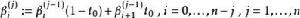德卡斯特里奧算法
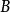德卡斯特里奧算法
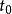德卡斯特里奧算法
德卡斯特里奧算法
德卡斯特里奧算法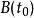
德卡斯特里奧算法然後， 在 點上的計算可以此算法的 步計算。 的結果為：
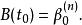德卡斯特里奧算法 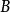德卡斯特里奧算法 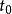德卡斯特里奧算法再者，貝茲曲線 可在 分成帶有各種控制點的兩段曲線：
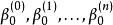德卡斯特里奧算法注意事項
進行手算時把係數寫成三角形形式很有用。
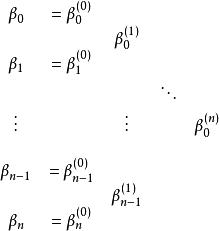德卡斯特里奧算法當選擇一點t0來計算波恩斯坦多項式時，我們可以用三角形形式的兩個對角線來構造多項式的分段表示。
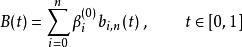德卡斯特里奧算法把它變成
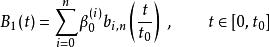德卡斯特里奧算法以及
例子
我們要計算2次波恩斯坦多項式，其伯恩斯坦係數為
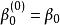德卡斯特里奧算法
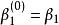德卡斯特里奧算法
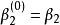德卡斯特里奧算法在t0點計算。
我們有下式開始遞歸
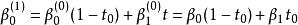德卡斯特里奧算法
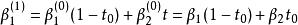德卡斯特里奧算法遞歸的第二次重複結束於
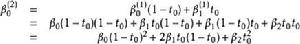德卡斯特里奧算法這就是我們所預料的n階伯恩斯坦多項式。
貝塞爾曲線
在計算帶n+1個控制點Pi的三維空間中的n次貝塞爾曲線 (Bézier curve) 時：
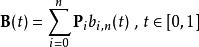德卡斯特里奧算法
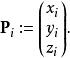德卡斯特里奧算法其中，
我們把Bézier曲線分成三個分立的方程：
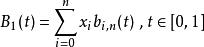德卡斯特里奧算法
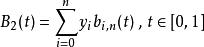德卡斯特里奧算法
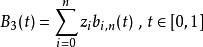德卡斯特里奧算法然後我們用de Casteljau算法分別計算。
偽代碼例子
這是一個遞歸的畫出一條從點P1到P4，彎向P2和P3的曲線的偽代碼例子。級數參數是遞歸的次數。該過程用增加了的級數參數來遞歸的調用它自己。當級別達到最大級別這個全局變數時，在P1和P4之間就畫上直線。函式中點（midpoint）去兩個點，並返回這兩點間的線段的中點。
