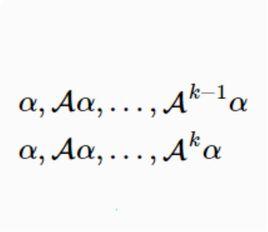基本介紹
 循環子空間
循環子空間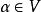 循環子空間
循環子空間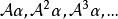 循環子空間
循環子空間設V是域F上線性空間, 是V的一個(固定)線性變換,設 ,而W是含α的最小不變子空間,那么W至少應含 ,故W至少應包含多項式對α的作用象
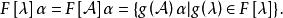 循環子空間
循環子空間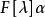 循環子空間
循環子空間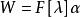 循環子空間
循環子空間而另一方面, 顯然已是不變子空間,故知 。
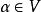 循環子空間
循環子空間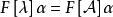 循環子空間
循環子空間 循環子空間
循環子空間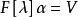 循環子空間
循環子空間定義1 (1)設 ,則 稱為α生成的 的 循環子空間(cyclic subspace)(這是含α的最小不變子空間)。(2)若V中有向量α使 ,則稱V是 循環空間,稱α是V的 循環向量 。
相關概念及性質
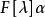 循環子空間
循環子空間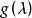 循環子空間
循環子空間為了查明 的大小,要查明有哪些多項式 化α為0,即
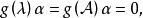 循環子空間
循環子空間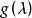 循環子空間
循環子空間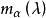 循環子空間
循環子空間這樣的多項式 稱為α的 零化子或 零化多項式(annihilator),α的次數最低的首一零化多項式 稱為α的 最小零化子。容易證明零化多項式恰為最小零化子的多項式的倍,最小零化子可按以下方法求得。依次查
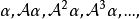 循環子空間
循環子空間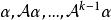 循環子空間
循環子空間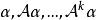 循環子空間
循環子空間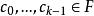 循環子空間
循環子空間可求得正整數k使得 線性無關而 線性相關,即有 使
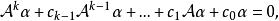 循環子空間
循環子空間即
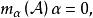 循環子空間
循環子空間其中
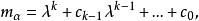 循環子空間
循環子空間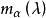 循環子空間
循環子空間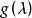 循環子空間
循環子空間於是 是α的零化多項式,若 是α的零化多項式,而
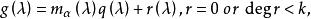 循環子空間
循環子空間則
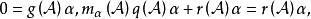 循環子空間
循環子空間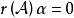 循環子空間
循環子空間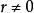 循環子空間
循環子空間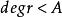 循環子空間
循環子空間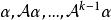 循環子空間
循環子空間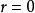 循環子空間
循環子空間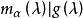 循環子空間
循環子空間所以 ,若 ,則 ,這與 線性無關矛盾,故 ,即 。
 循環子空間
循環子空間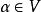 循環子空間
循環子空間定理1 設V是域F上n維線性空間, 是V的線性變換,固定 ,記α生成的循環子空間為
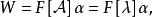 循環子空間
循環子空間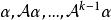 循環子空間
循環子空間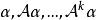 循環子空間
循環子空間(1)若 線性無關,而 線性相關,設為
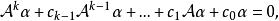 循環子空間
循環子空間則
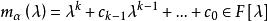 循環子空間
循環子空間是α的最小零化子;
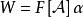 循環子空間
循環子空間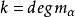 循環子空間
循環子空間(2) 的維數為是 ,且
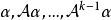 循環子空間
循環子空間是W的基。
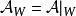 循環子空間
循環子空間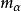 循環子空間
循環子空間(3) 在上述基下的方陣表示為 的友陣
 循環子空間
循環子空間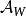 循環子空間
循環子空間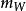 循環子空間
循環子空間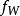 循環子空間
循環子空間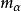 循環子空間
循環子空間特別地, 的最小多項式 、特徵多項式 及α的最小零化子 三者相等,即
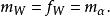 循環子空間
循環子空間證明 (1)已證。
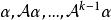 循環子空間
循環子空間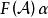 循環子空間
循環子空間(2)已證明 線性無關,只要再證明 中任一向量均可由它們線性表出,已知
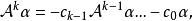 循環子空間
循環子空間 循環子空間
循環子空間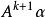 循環子空間
循環子空間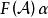 循環子空間
循環子空間兩邊同以 作用,可得 能由它們表出,如此遞推可知 可由它們表出。
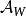 循環子空間
循環子空間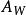 循環子空間
循環子空間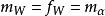 循環子空間
循環子空間(3)顯然, 的方陣為 ,由友陣的性質即知 。
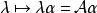 循環子空間
循環子空間註記 定理1的抽象證明:考慮線性映射 ,即
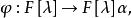 循環子空間
循環子空間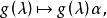 循環子空間
循環子空間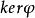 循環子空間
循環子空間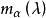 循環子空間
循環子空間其核 由 的倍全體組成 :
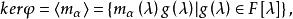 循環子空間
循環子空間故由線性映射基本定理有
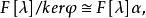 循環子空間
循環子空間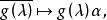 循環子空間
循環子空間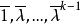 循環子空間
循環子空間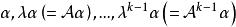 循環子空間
循環子空間左端的基是 ,故右端的基是 。