基本介紹
古埃及數字(ancient Egyptian numerals)是古代人類最重要、最基本的數字之一。指古埃及人創造的一種十進制象形文數字。約公元前4000年,埃及就已有了相當發達的文化,當時已有了象形文字,現在尚存於英國牛津博物館的埃及王室的權標;存於莫斯科國立普希金造型藝術博物館裡的莫斯科數學紙草書;存於英國博物館的萊因德紙草書;存於法國盧佛爾博物館的羅林紙草書(尼羅河三角洲上生長的一種形似蘆葦的植物,把莖逐層撕開為薄片,古代用以著書,稱紙草書),上面都寫有古埃及的象形文字,或另一種 僧侶文字。象形文數字形如下圖:
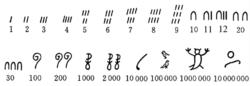 圖1
圖1 古埃及象形文數字用的是十進制記數法,由於沒有位值制,所以數的記法比較麻煩,有多少個單位就要重複多少次,如24記為
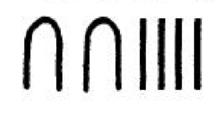 圖2
圖2 像986這個數,需要用23個符號來表示,除了象形文數字外,古埃及還有宗教文字,一般稱為 僧侶文,下面列出僧侶文的數字 。
 埃及數字
埃及數字  埃及數字
埃及數字 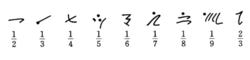 埃及數字
埃及數字 數字的名稱及符號
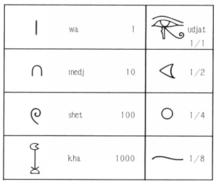
古埃及人將1~9個數字分別稱為wa,senuj,khemet,jfedu,dju,sjsu,sefekhu,khemenu,pesedshu。古埃及人稱10為medshu,並且用形如“軛”的符號來表示;稱100為shenet,用一圈繩子表示;稱1 000為kha,用一枚蓮花表示;稱10 000為dsheba,用一個指頭表示;稱100 000為hefen,用一隻蝌蚪表示;稱1 000 000為heh,用舉著兩條胳膊端坐著的神來表示。記載日期和計數時所用的序數通過在基數後面加後綴-nu或者前面加前綴mech-來表示 。
 埃及數字
埃及數字 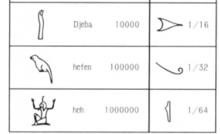 埃及數字
埃及數字 相關介紹
大約在公元前3100年左右, 埃及人沿尼羅河兩岸建立了統一的國家,與此同時發明了象形文字。在一根當時的王室權標上,用象形文字記載著幾個以百萬和十萬計的大數。尼羅河的定期泛濫,使人們每年都要重新丈量耕地面積。從公元前2900年左右開始, 埃及人建造了許多巨大的金字塔,其測量精度是驚人的。因此,埃及人很早就有了豐富的算術與幾何知識。根據大約公元前1850—前1650年間的兩份紙草書 (參見“莫斯科紙草書”、“阿默斯紙草書”)人們進一步了解到埃及古代數學的豐富內容 。
埃及人建立了以10為基數的數字元號。由於完全沒有位值的概念,他們需要為10的每一冪次設計一個新的符號,這些符號大致如下:
 埃及象形數字
埃及象形數字 一般數字是將10的各個冪次按加法原則累積而成,這使得數的表示與各種運算都十分煩瑣。大約在中王國時期(約公元前2133—前1786)。由象形文字演變出一種 僧侶文字,在寫法上簡化了許多,前面提到的兩種紙草書就是用這種文字寫成的, 其中的數字元號寫法是:
 埃及僧侶數字
埃及僧侶數字 埃及人掌握了完整而正確的加減乘除運算方法。由於數字記法的累加性, 加減法可以直接通過添加或去掉一些符號而完成。乘法相當煩瑣。他們發明了形如1/n(n是自然數)的單位分數。一般分數均表示為單位分數的和,為此編制了專門的分解表。除法是根據乘法的逆運算原理或利用分數分解表實現的。
埃及人解決了一些在今天看來屬於代數學範圍的問題。他們的 “堆算”常被認為是一元一次方程。約公元前1950年的卡洪Kahun紙草書中的一個問題則被認為是二次方程,原題是:“把一個面積為100的正方形分為兩個較小的正方形, 使其中個的邊長是另一個的3/4”。還有的問題涉及等差與等比數列中的幾項。但是,所有這些問題都是用加、減、乘、除、比例等典型的算術方法求解的,至多涉及開平方運算,其典型方法是基於比例原理的試位法(參見該條), 很難說其中已經包含了代數學的思想與方法。
埃及人有著豐富的幾何知識, 他們正確地計算了正方形、長方形、直角三角形,等腰三角形、直角或等腰梯形,以及可以分解為這些圖形的田地面積,他們的圓面積(參見該條)公式相當於圓周率取3. 16049,這在當時是了不起的成就。他們也正確地計算了立方體、長方體、稜柱、圓柱的體積,特別是以對稱的形式給出了正四稜台的體積公式(參見“莫斯科紙草書”),他們的圓台、半球體積公式卻是相當粗糙的。
埃及古代數學基本上仍然是一門實用技術。其結果仍然是經驗性的, 但這些內容對於後世數學的發展又是必不可少的, 輝煌的希臘古代數學正是在繼承了巴比倫與埃及的豐富遺產之後發展起來的 。
 重量的表示
重量的表示 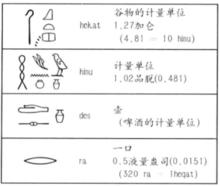 容量的表示
容量的表示 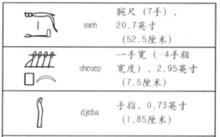 長度的表示
長度的表示 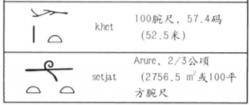 長度及面積
長度及面積 
