基本介紹
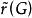圈基圈基是圖G的循環空間(參見下文“點空間”)的一組基，循環空間的維數稱為圈秩或簡稱上秩，記為 ，
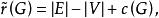圈基
圈基
圈基
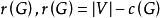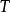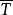圈基 圈基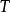
圈基 圈基其中 為 的連通片數。上循環空間的一組基稱為上圈基，上循環空間的維數稱為上圈秩或簡稱秩，記為 。若 為圖 的一個支撐樹， 為相應的上樹，則任何一個上樹邊與樹恰形成一個圈，稱為樹 的一個基本圈。相仿地，每一個樹邊與上樹恰形成一個上圈，稱為樹T的一個基本上圈。支撐樹T的所有基本圈構成圖G的一個圈基，所有基本上圈構成圖G的一個上圈基。雙循環空間的一組基稱為雙圈基，雙循環空間的維數稱為雙圈秩，與某一雙圈基中的每一個圈恰有一條公共邊的邊集，稱為雙樹 。
相關概念
點空間
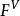圈基
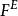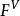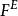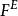圈基 圈基 圈基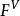 圈基 圈基點空間(vertex space)是一類組合構形，指由圖G=(V，E)的頂點集V生成的域F(通常取二元域)上的向量空間，記為 。由邊集E生成的域F上的向量空間稱為邊空間，記為 。 中的向量稱為0鏈， 中的向量稱為1鏈。邊緣運算元是由 到 的一個線性變換，它將任一邊映射為其兩端點的和。 上邊緣運算元是由F到F的一個線性變換，它將任一頂點映射為與其關聯的所有邊的和，邊緣運算元的像空間稱為 邊緣空間，它的核空間稱為 循環空間。上邊緣運算元的像空間稱為 上循環空間，循環空間與上循環空間的交空間稱為 雙循環空間。若兩個0鏈 在上邊緣運算元作用下具有相同的像，則稱它們 上同調。若兩個1鏈在邊緣運算元作用下具有相同的像，則稱它們 同調。
生成樹
連通且無簡單迴路的無向圖稱為 無向樹，簡稱樹。樹中度數為1的頂點稱為 樹葉，度數大於1的頂點稱為 分支點或內點，僅含一個孤立點的樹稱為 平凡樹，無簡單迴路的無向圖稱為 森林。
定理1設圖T有n個頂點，則下述命題相互等價。
(1)T是樹；
(2)T是無迴路的圖，且e=n-1，其中e是圖的邊數；
(3)T是連通圖且e=n-1；
(4)T是無同路圖，且在T中任意兩個不相鄰的頂點之間添加一邊後，恰得一條迴路(這時稱T為最大無迴路圖)；
(5)T連通，但是刪去任何一邊後便不再連通(這時稱T為最小連通圖)；
(6)T的每一對不同頂點之間有唯一的一條路。
若連通圖G的生成子圖是一棵樹，則稱這棵樹為G的 生成樹。
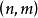圈基設G是一個 -連通圖，則相對於它的任何一個生成樹T，含有m-(n-1)個補樹邊，根據定理1中命題(4)，對每條補樹邊e，T+e有且僅有一個圈，因此G中至少含有m-n+1個圈，這m-n+1個圈是G的基本圈，構成G的圈空間的基，因而又稱m-n+1為G的 圈秩。
定理2 設T是連通圖的G的生成樹。則(1)G的任何邊割集與T至少有一公共邊；(2)G的任何圈與補樹至少有一條公共邊 。
秩多項式
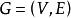圈基對於圖 ，記
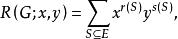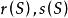圈基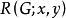
圈基
圈基其中， 分別為以S為邊集的G的支撐子圖的秩和上秩，稱 為圖G的 秩多項式。
