合一算法簡介
非形式地講,合一就是確定將兩個表達式e和f中的變數用相應的表達式替換後能否變成等價表達式的問題。測試表達式相等是合一的特殊情況。如果e和f中只包含常量而沒有變數,則若且唯若e和f完全相同時e和f合一。本節的合一算法可以用於帶環圖,所以該算法可用於測試存在環類型的結構等價。
合一是基於稱為代換的函式S(從變數到表達式的映射)來定義的。如果將e中的每個變數a均用S(a)代換,則得到的表達式記為s(e)。如果S(e)=S(f),則稱s為e和f的合一代換。本節的算法旨在確定這樣一種代換:它是一對表達式上的最一般的合一代換。
研究集合{P(a),P(x)}。集合中的兩個表達式是不同的,差別是在P(a)中出現a,而在P(x)中出現x。為了求出該集合的合一置換,應首先找出兩個表達式的不一致之處,然後再試圖消除。對P(a)和P(x),不一致之處可用集合(a,x)表示。由於x是變數,可以取θ={a/x),
於是有
 合一算法
合一算法即θ是(P(n),P(z))的合一置換。這就是合一算法所依據的思想。在討論合一算法之前先討論差異集的概念。
差異集
定義:表達式的非空集合W的差異集是按下述方法得出的子表達式的集合。
(1)在w的所有表達式中找出對應符號不全相同的第一個符號(自左算起)。
(2)在w的每個表達式中,提取出占有該符號位置的子表達式。這些子表達式的集合便是W的差異集D。
非空表達式集W的差別集:
從左向右,在W中的所有表達式,遇到第一個不相同符號,提取從這個符號開始的子表達式,由此構成一個集合,稱為W的差別集,記為D。
例子:
W={P(x,f(y,z),z,w),P(x,a),P(x,g(z),z,b)}
D={f(y,z),a,g(z)}
最一般合一子
最一般合一子(mostgeneralunifier,mgu)
定義:如果對E的每個合一子θ,都存在一個置換λ,使得θ=γ°λ,則稱合一子γ是集合{E1,…,En}的最一般合一子.
例子:
E={P(x,y),P(x,f(b))},θ1={a/x,f(b)/y},θ2={b/x,f(b)/y}
最一般合一子γ={f(b)/y}
θ1=γ°{a/x},θ2=γ°{b/x}
合一算法的考慮
消除兩個謂詞之間項的差別:{P(x,…),P(a,…)}
W的合一算法:
1.K=0,Wk=W,γk=ε.
2.如果Wk是單一的,停機,γk是W的mgu.
否則,求出Wk的差別集Dk.
3.如果在Dk中存在元素vk與tk,使vk是一個未出
現在tk中的變數,轉4;
否則,停機,W是不可合一的.
4.令γk+1=γk°{tk/vk},Wk+1=Wk
°γk+1.
5.K=K+1.轉2.
算法實現
要將合一的基於圖論的形式化描述實現為算法,關鍵是將最一般的合一代換下等價的兩個表達式所對應的結點進行分組。兩個表達式由圖中標記為“→:1”的兩個結點表示。在結點1被合一之後,結點上的整數表示結點所屬的等價類編號。
等價類
等價類具有如下性質,即同一等價類中的所有內結點表示相同的操作符。在一個等價類中,內部結點對應的子結點也都是等價的。
 合一算法
合一算法過程
圖中一對結點的合一。
輸入:一個圖和一對要合一的結點m和n。
輸出:如果結點m和11所表示的表達式合一,則輸出布爾值true,否則輸出false。如果算法中的函式不是返回false,而是改為導致失敗,那么該算法就是圖5.15中類型檢查規則所需的unify(合一)的另一版本。
方法
結點用圖中的記錄來表示,該記錄包含一個二元操作符域和指向左右兒子的指針。
 結點的數據結構
結點的數據結構等價結點
等價結點的集合用set域來保存。每個等價類都選擇一個結點作為該等價類的惟一代表,該結點的set域置為空指針,等價類中其他結點的set域均指向(可能間接地通過集合中的其他結點)這個代表結點。初始時,每個結點n的等價類就是自身,而且n也是其自身的代表結點。
具體算法
合一算法使用了下面兩個作用在結點上的操作。
(1)find(n)。返回結點n當前所在等價類的代表結點。
(2)union(m,n)。合併結點m和n所在的兩個等價類。如果兩個等價類中的某一代表結點是非變數結點,那么union將該結點作為合併後等價類的代表結點。
否則union任選其中的一個作為新的代表結點。在union的說明中,這種非對稱性很重要,因為變數不能當作一個包含類型構造符或基本類型的表達式的等價類代表。否則,兩個等價的表達式就可以通過該變數合一。
集合上的union操作可通過修改其中一個等價類的代表上的set域,使其指向另一等價類的代表來實現。為尋找某結點所屬的等價類,逐級查找結點的set指針,直到到達代表結點(該結點的set域為空指針)為止。
注意
圖中r的算法分別使用s=find(m)和t=find(n),而不是m和n。如果m和n在同一等價類中,則代表結點8和t相等。如果s和t代表同一基本類型,則unify(m,n)返回true。如果S和t都是代表二元類型構造符的內部結點,先試著將其合併,然後遞歸地檢查它們各自的子結點是否等價。通過先進行合併,在遞歸檢查子結點之前,等價類的數目就會減少,所以算法最終會停止。
用表達式代換變數是通過將代表變數的葉結點加到包含該表達式對應結點的等價類中來實現的。如果m或n是代表變數的葉結點,而且已經被加到某結點所屬的等價類中,而該結點是一個包含類型構造符或基本類型的表達式所對應的結點,那么其上的find將返回該類型構造符或基本類型的代表,所以此時變數不可能與兩個不同的表達式進行合一。
對有限非空可合一的表達式集合給出求取最一般合一置換的合一算法。當集合不可合一時,算法也能給出不可合一的結論,並且結束。
合一算法
第1步置k=0,W=W,σ=ε。
第2步若W中只有一個元素,終止,並且σ為W的最一般合一。否則求出W的
差異集Dk。
第3步 若Dk中存在元素v和t,並且v是不出現在t中的變數,則轉向第4步。否則終止,並且W是不可合一的。
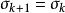 合一算法
合一算法第4步 置(注意w胖1=肋抖1)。
第5步置k=k+1,轉向第2步。
注意:在第3步,要求v不出現在t中的,這稱為occur檢查,算法的正確性依賴於它。但是由於occur檢查,使上述合一算法在最壞的情況下運行時間是輸入長度的指數函式,因此在多數Prolog程式設計系統中都省略了occur檢查。
置換(substitution)和合一的區別
定義:置換是一個形如{t1/v1,…,tn/vn}的有限集,其中每個vi是變數,ti是不同於vi的項(常量、變數或函式)(vi≠ti).當i≠j時,vi≠vj.
無元素組成的置換稱為空置換,記為ε;
例子:
{a/x,w/y,f(s)/z},{g(x)/x}是置換;
{x/x},{y/f(x)}不是置換;
概念的理解:
置換:被置換元素必是變數,置換元素是項;
置換元素必不同於被置換元素;
在一次置換中,針對同一元素的置換隻能出現一次(單次置換的同時性);
無元素組成的置換,成為空置換;
