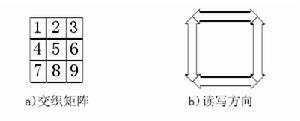
原理
一個比較簡單的3×3交織矩陣可以看出一共有32種交織方式的存在，然而這32種讀法中雖然有許多在形式上不同，但就其本質來講所表現的特性卻是完全一致的。所以它們又可以歸納為有限的四種形式，我們用L代表左，R代表右，T代表上，B代表下，則這四種交織器依次可以表示成:LR/TB,LR/BT,RL/TB,RL/BT。
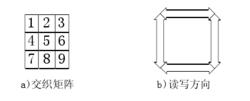交織器原理圖其中LR表示由左至右寫入，TB表示由上至下讀出，對於如圖所示交織器：LR/TB置換表示為:(1 2 3 4 5 6 7 8 9)
(1 4 7 2 5 8 3 6 9)
LR/BT置換表示為:(1 2 3 4 5 6 7 8 9)
(7 4 1 8 5 2 9 6 3)
RL/TB置換表示為:(1 2 3 4 5 6 7 8 9)
(3 6 9 2 5 8 1 4 7)
RL/BT置換表示為:(1 2 3 4 5 6 7 8 9)
(9 6 3 8 5 2 7 4 1)
從上例我們可以很容易的看出當M=N時，LR/TB和RL/BT置換是自反的。
作用
交織器通常是對輸入的原始信息序列進行隨機置換後從前向後讀出。交織使編碼產生隨機度，使碼隨機化、均勻化，它只起著對碼重量整形的作用。在解碼端，對於某一個子解碼器來說不可糾正的錯誤事件，交織後在另一個解碼器被打散，成為可糾正差錯。
設計
交織器設計的目標是使交織前後的序列的相關性越小越好。如果交織前後的信息序列是統計獨立的，則相關係數為零。只有當序列X和Y中的同一位置上的元素同時取“0”或“1”時才使序列的相關性加大。對輸入信息序列而一言，其相關性發生在交織前後比特位的不動點以及交織前後同一位置的信息比特取相同值的情況下。從統計學的角度來進行分析，上面提到的交織器對相關係數的影響是一致的，故僅需要計算在交織過程中不動點的個數的多少。對於長為n的序列，當M=N時，LR/TB和LR/BT型交織器的不動點分別發生在矩陣的對角線和斜對角線上，個數均為N個;而當M≠N時，LR/TB型交織器的不動點個數遠遠少於LR/BT型交織器。例如對於13*15型交織器，在交織過程中，LR/TB型交織器的不動點個數為3，而LR/BT型交織器僅有一個不動點。從理論上來說，採用LR/BT型交織器的效果要比用LR/TB型交織器的解碼效果好。
