基本介紹
 出度
出度 出度
出度 出度
出度在無向圖中,頂點所具有的邊的數目稱為頂點的 度。如圖1(a)中.無向圖的頂點的度為3,頂點的度為2。
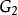 出度
出度 出度
出度 出度
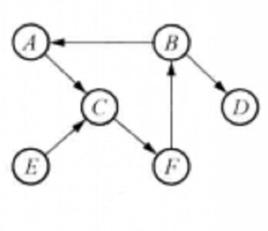
出度在有向圖中,以頂點為頭的邊的數目稱為該頂點的 入度;以頂點為尾的邊的數目稱為該頂點的 出度;一個頂點的入度與出度之和稱為該頂點的 度。如圖1中,有向圖的頂點的入度為2,出度也是2,頂點的度則為4。
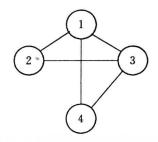 圖1(a)G₁
圖1(a)G₁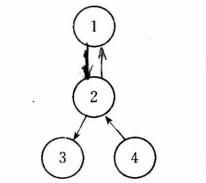 圖1(b)G₂
圖1(b)G₂ 出度
出度 出度
出度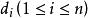 出度
出度設無向圖有個頂點,e條邊,每個頂點的度為,則有 :
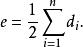 出度
出度相關概念
圖的定義
 出度
出度 出度
出度 出度
出度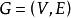 出度
出度一個圖由一個非空有限頂點集和一個邊的有限集組成。圖的頂點集和邊集分別用和表示,則圖G可表示成。
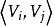 出度
出度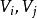 出度
出度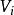 出度
出度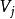 出度
出度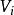 出度
出度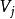 出度
出度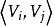 出度
出度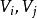 出度
出度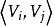 出度
出度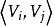 出度
出度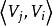 出度
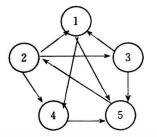
出度在圖中,若每條邊都用箭頭指明了方向,則稱此圖為 有向圖,否則為 無向圖。有向圖中的邊用表示,其中是有向圖的兩個頂點,稱為尾,稱為頭,在有向圖中用從到的箭頭表示,見圖2(a)。無向圖中的邊用表示,為無向圖的兩個頂點。圖2(b)是無向圖。無向圖的邊是無序的,也就是說與表示同一條邊。
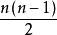 出度
出度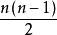 出度
出度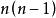 出度
出度從圖2中可知,(b)是一棵樹,而(a)不是樹,所以說樹是圖的特例。具有n個頂點的無向圖,若有條邊,稱之為 完全圖。圖2中(c)便是一個完全圖。具有n個頂點的無向圖,至多有條邊;具有n個頂點的有向圖,則至多有條邊 。
 出度 出度 | 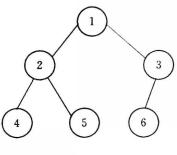 出度 出度 | 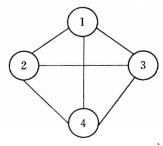 出度 出度 |
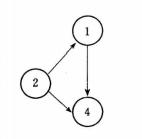 出度 出度 |  出度 出度 | 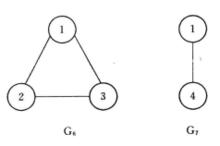 出度 出度 |
子圖
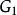 出度
出度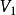 出度
出度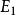 出度
出度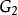 出度
出度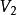 出度
出度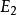 出度
出度設圖的頂點集和邊集為和,圖的頂點集和邊集為和,若:
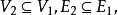 出度
出度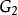 出度
出度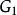 出度
出度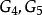 出度
出度 出度
出度 出度
出度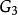 出度
出度則稱圖是圖的子圖。例如,圖2中圖是圖的子圖,圖是圖的子圖 。